Cet article est composé de trois parties. Cette partie constitue la troisième des trois. Pour aller lire (ou relire) la première partie, clique ici, la deuxième partie clique ici.
Cette troisième et dernière partie est, comme l’ont été les deux premières, richement illustrée dont plusieurs très courtes vidéos. Mets bien ainsi le son de ton ordinateur en route dès maintenant.
Rappelle toi, en fin de deuxième partie, nous en étions restés à :
Que se passe-t-il aux pôles ?
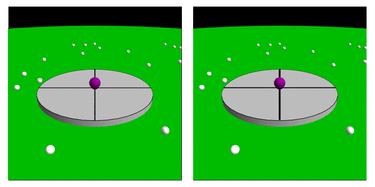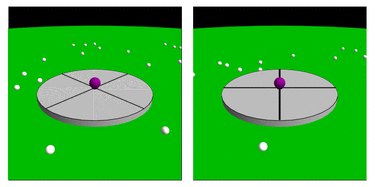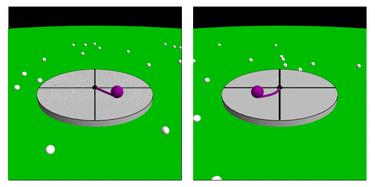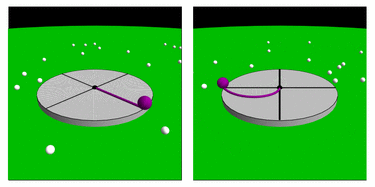
Au pôle Nord (latitude : 90° Nord) la verticale du point de suspension du pendule coïncide avec l’axe de rotation de la Terre, autrement dit, le plan d’oscillation du pendule est en rotation autour de l’axe de la verticale du lieu. Un observateur tourne avec la Terre et reste fixe par rapport au sol. Pour lui c’est l’axe d’oscillation du pendule qui tourne.
Ce même observateur qui se trouve ainsi au pôle Nord fait le tour complet en 24 heures (plus exactement en un jour sidéral, soit 23 heures 56 min), dans le sens horaire (c’est-à-dire dans le sens inverse de la rotation de la Terre), par rapport au plan d’oscillation du pendule (dont on reprécise que ce plan d’oscillation ne change jamais de direction quel que soit la direction dans laquelle il est lancé).
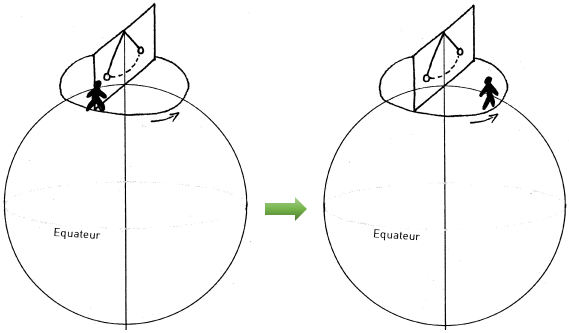
Le pendule oscille dans un plan fixe par rapport aux étoiles alors que dessous, la Terre tourne indépendamment. Sa vitesse de rotation est d’environ 15° par heure.
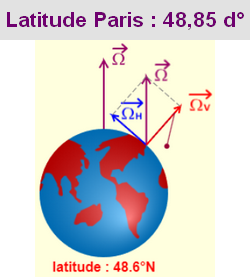
Pour ceux que cela intéresse le vecteur Ω est la composante verticale de la rotation de la Terre, décomposé en ΩV (verticale) et ΩH (horizontale).
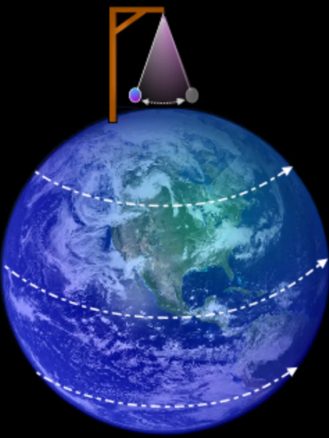
Au pôle Sud (latitude : 90° Sud), il se passe la même chose mais dans le sens inverse, it is not complicado !
Latitudes intermédiaires
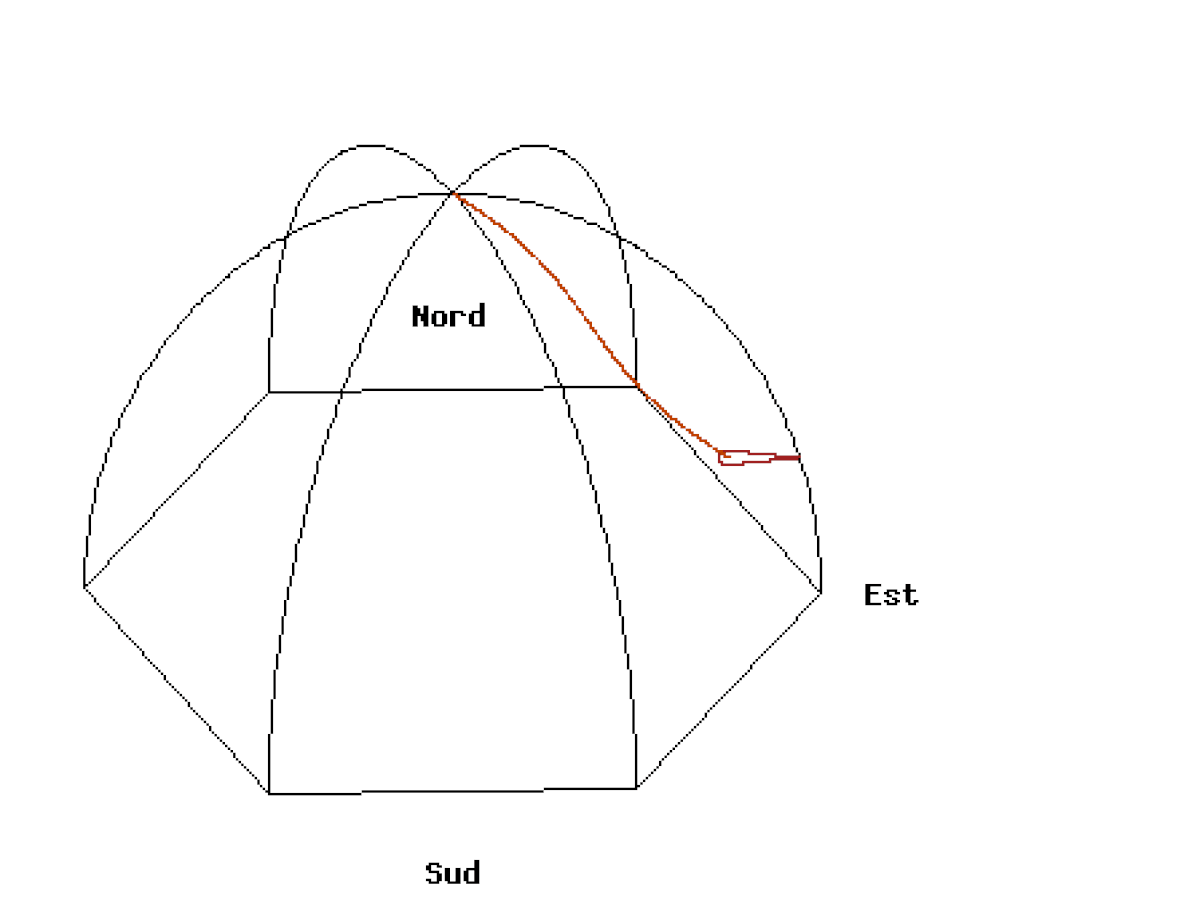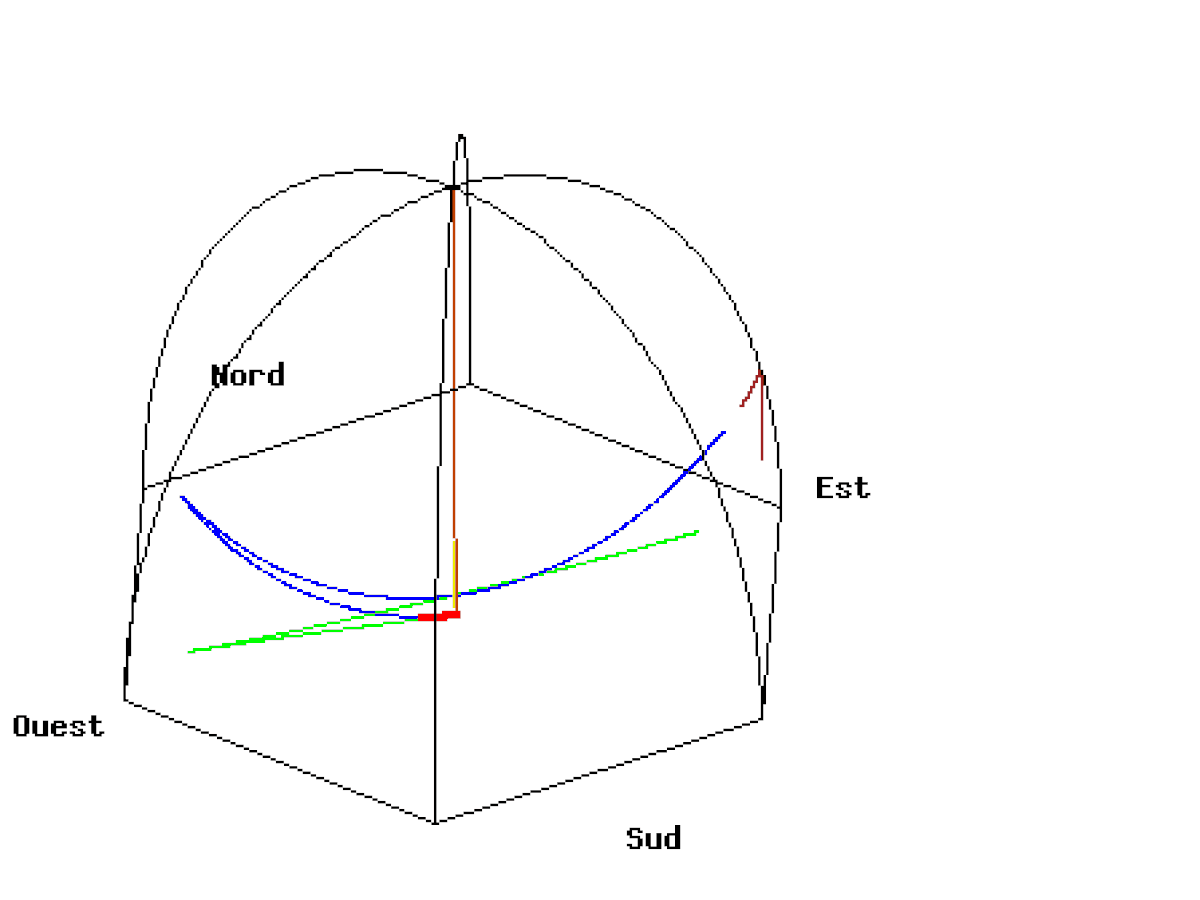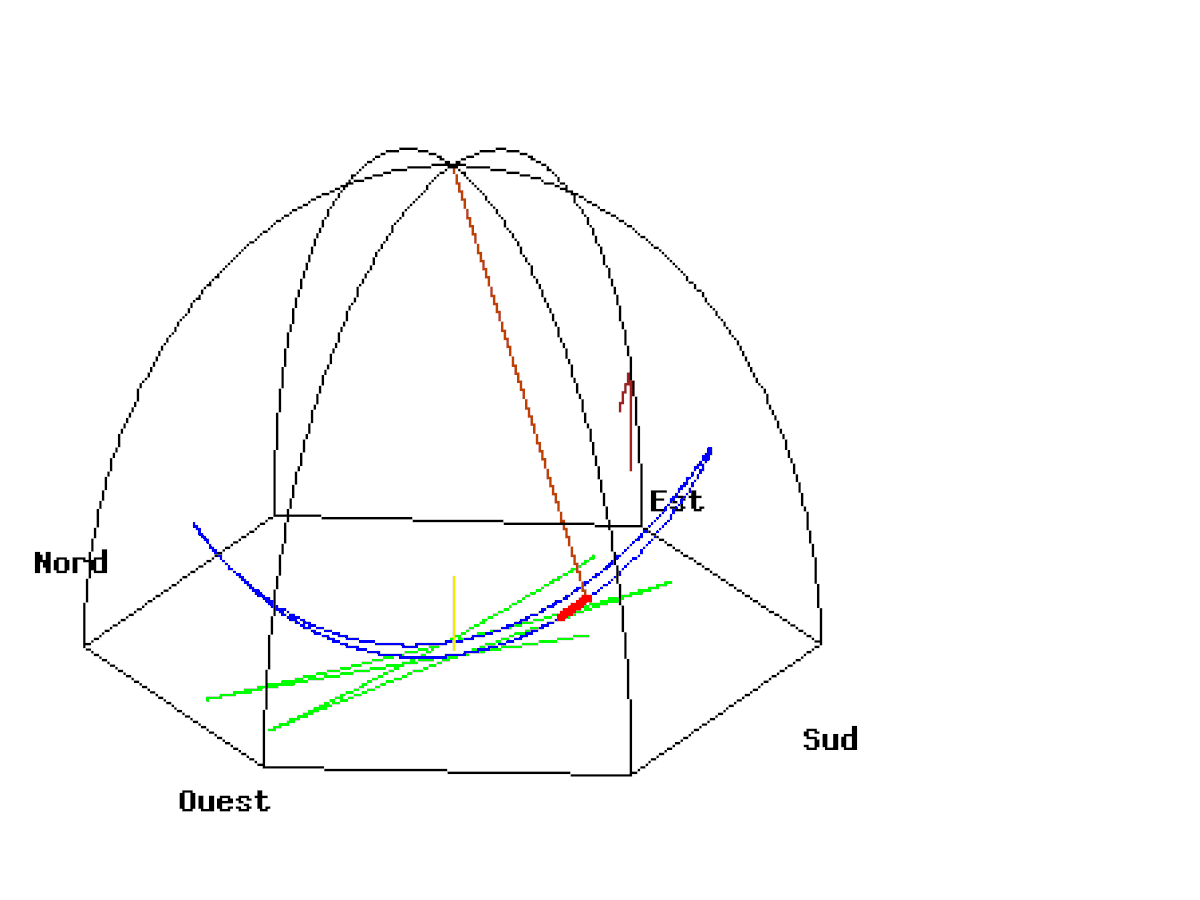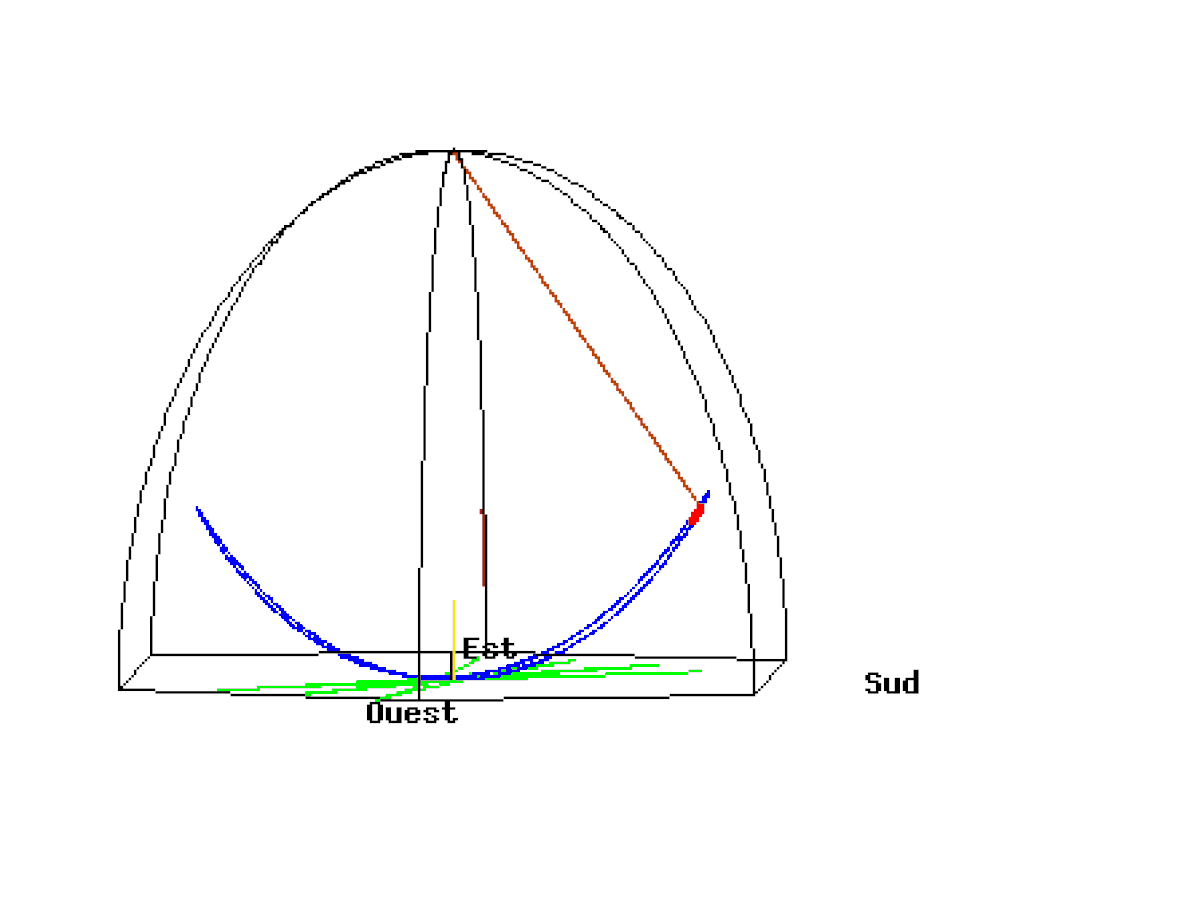
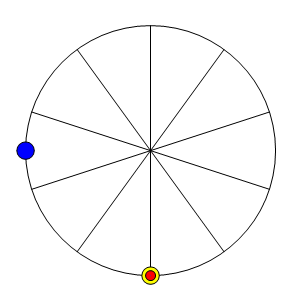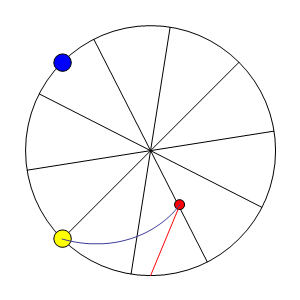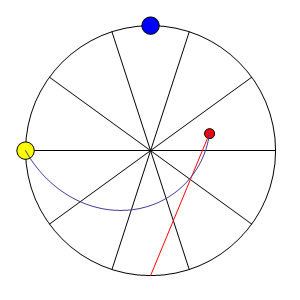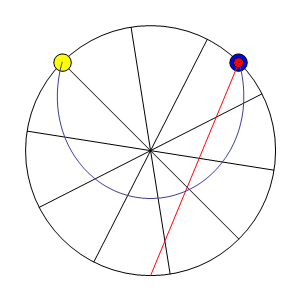
Plus la latitude se rapproche de l’équateur terrestre et plus les pendules mettent du temps pour revenir sur leur axe initial. Commençons par une position hors pôle et hors équateur, soit à une latitude quelconque.
À une latitude donnée le pendule n’oscille pas dans l’axe de rotation de la Terre. Il y a obligatoirement un angle qui est défini par la latitude.
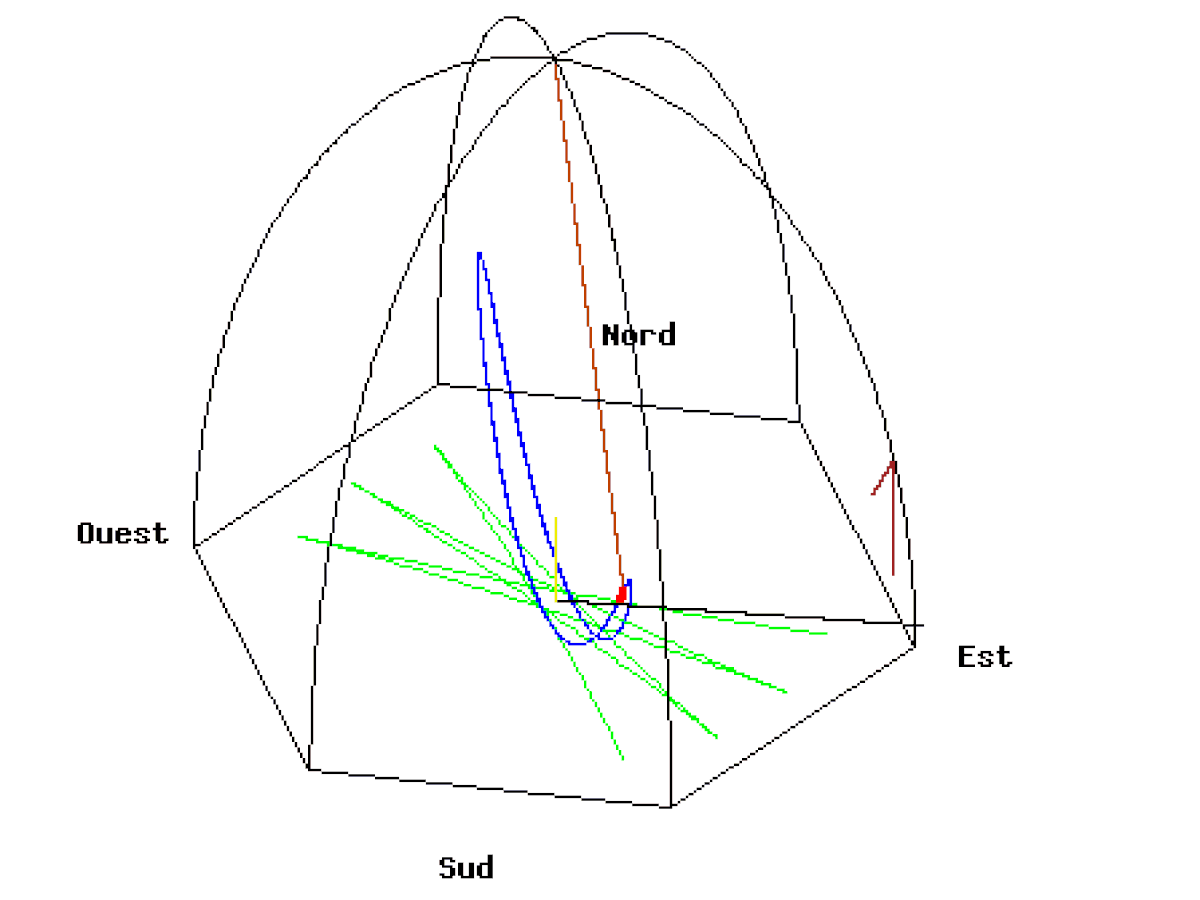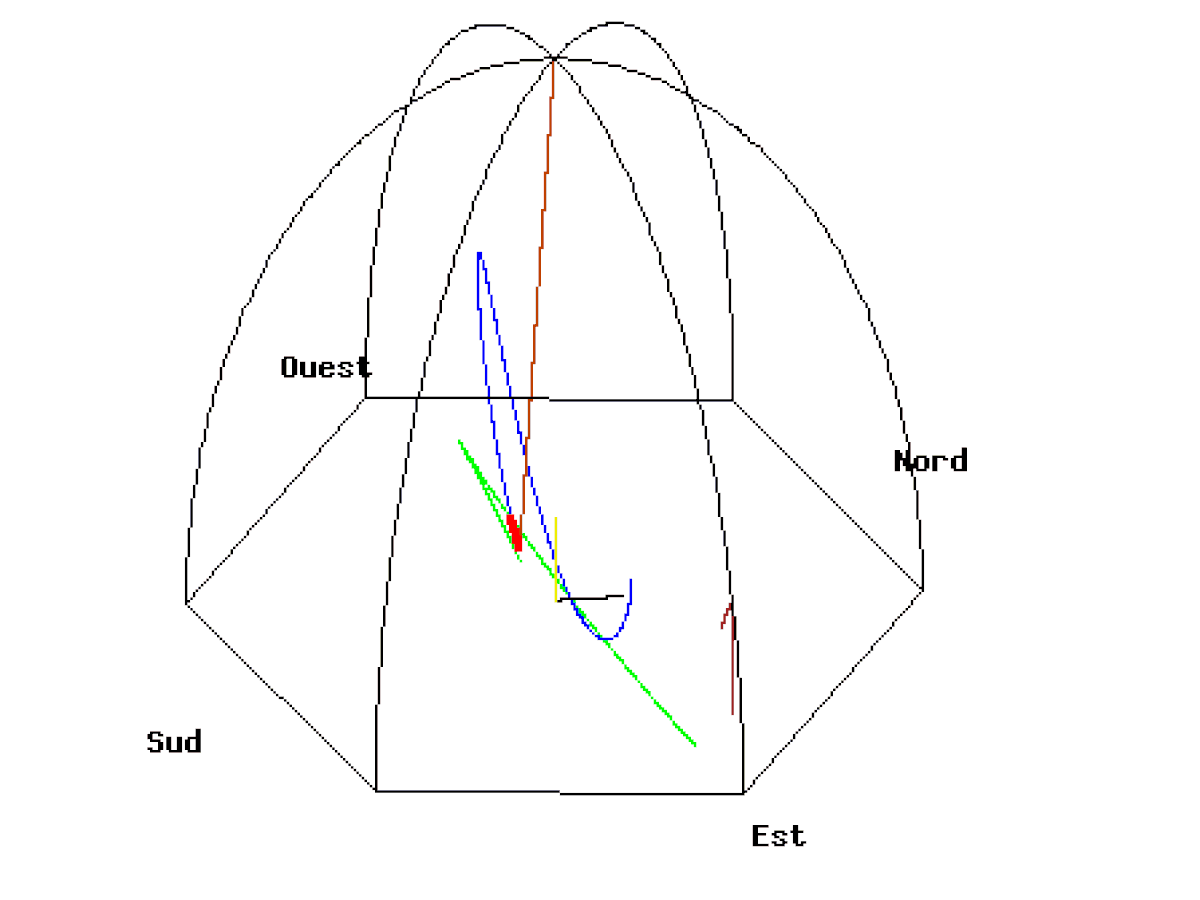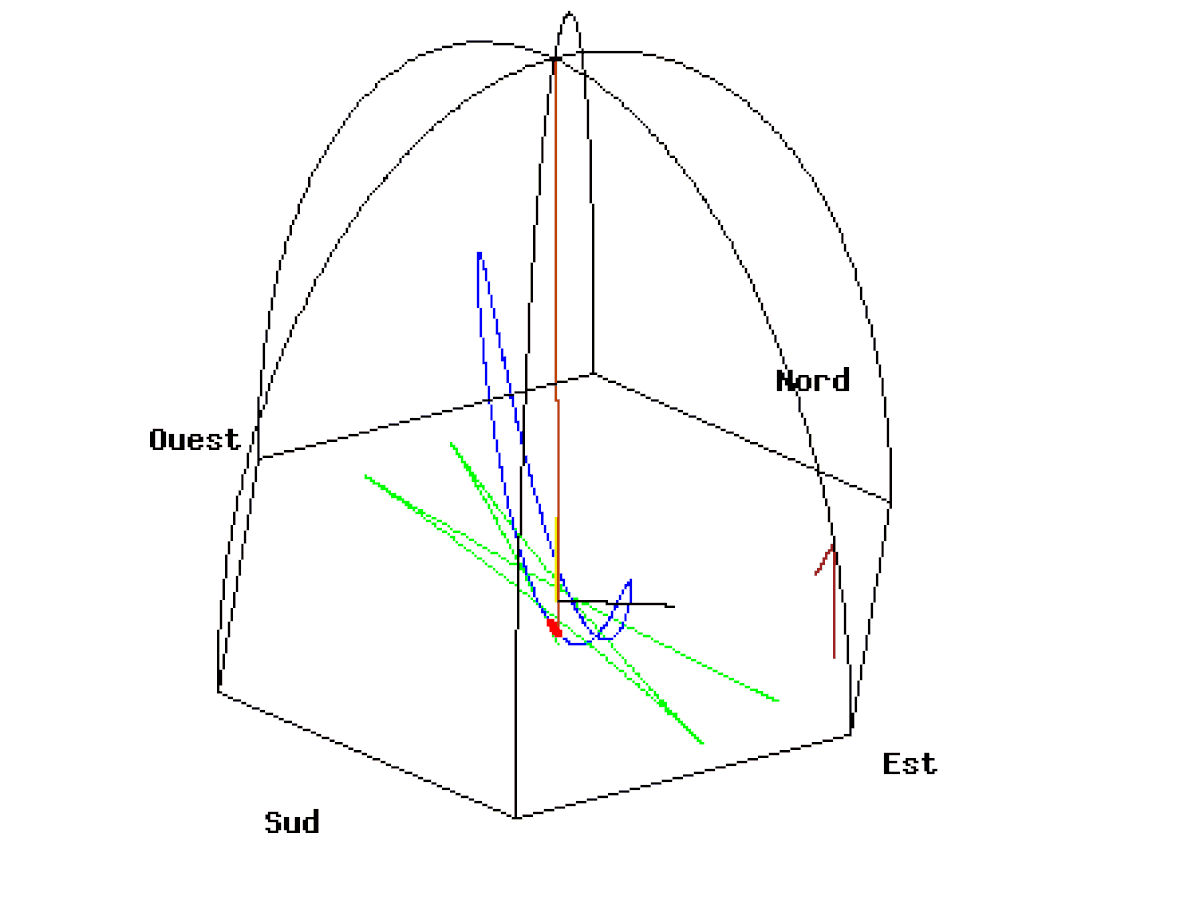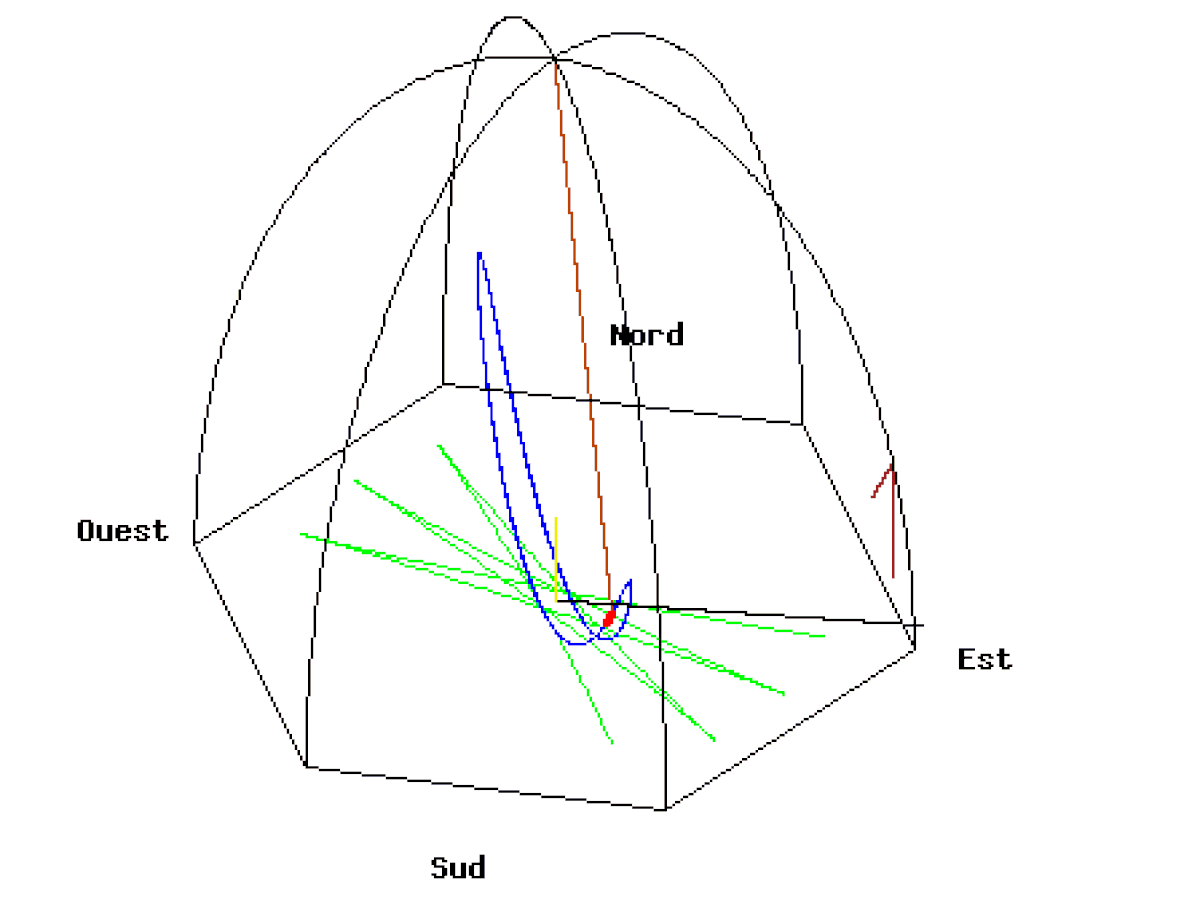
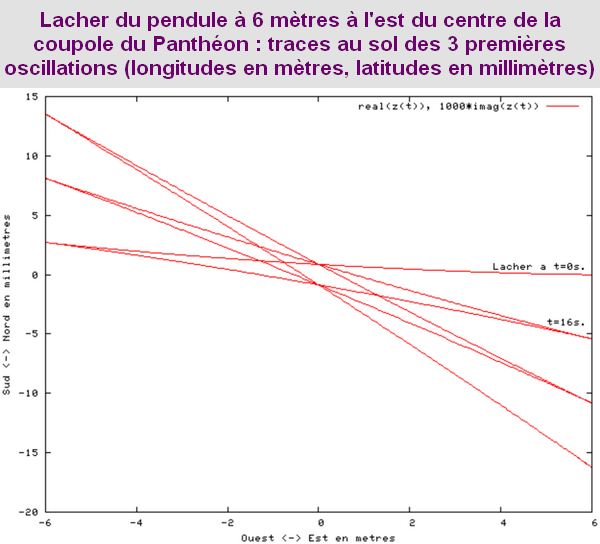
A Paris, le plan du pendule ne revient pas à son point de départ en 24 heures comme on pourrait le croire. A chaque oscillation de 16,42 secondes il se déplace de 5,4 mm dans le sens des aiguilles d’une montre (dans le sens inverse de la rotation de la Terre) et retrouve son point de départ en 31h 48′. Ce n’est pas le plan du pendule qui tourne mais la Terre.
Pour ceux que cela intéresse le vecteur Ω est la composante verticale de la rotation de la Terre, décomposé en ΩV (verticale) et ΩH (horizontale).
Ci-dessous, deux animations du Pendule de Foucault de 67 mètres lâché au Panthéon de Paris à une distance de 50 mètres à l’est du point d’équilibre avec une vitesse initiale nulle. La vitesse de rotation de la Terre est exagérée (1 tour en 110 secondes). Vue d’une caméra liée au plan d’oscillation.
A l’équateur
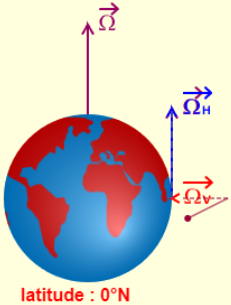A l’équateur le pendule finit par osciller dans un plan apparemment figé qui ne permet pas de voir la rotation de la Terre. Cette fois-ci, la verticale du pendule est perpendiculaire à l’axe de rotation de la Terre. Le pendule conserve la même direction, puisqu’il reste toujours perpendiculaire à l’axe de rotation. Ainsi, contrairement à ce qui se passe aux pôles, le sol ne tourne pas autour de l’axe du pendule mais transporte l’axe avec lui. Pour un observateur tout se passe comme si le pendule était transporté dans un train et se balançait dans le sens de la marche du train. Le plan du pendule est figé et la Terre ne tourne plus autour. Sa période de révolution tend vers l’infini.
Pour ceux que cela intéresse le vecteur Ω est la composante verticale de la rotation de la Terre, décomposé en ΩV (verticale) et ΩH (horizontale).
La force de Coriolis
Il ne semble pas que Foucault ait été informé des travaux de Coriolis portant sur les lois de la dynamique dans un référentiel non inertiel, datant de 1832. C’est donc de manière purement empirique qu’il mena son expérience, et seulement après coup que les mécaniciens expliquèrent l’expérience par l’utilisation de la force de Coriolis. Si le principe général fut rapidement expliqué, il fallut attendre, quand même, beaucoup plus longtemps pour en comprendre toutes les subtilités.
Qu’est-ce que la force de Coriolis ?
La force de Coriolis est un phénomène physique qui se produit quand un objet bouge au sein d’un système de référence en rotation, comme la Terre par exemple.
On précise un peu plus :
On précise encore un peu plus. On peut dire que la force de Coriolis est une pseudo-force qui apparaît dans un référentiel en rotation R’ par rapport à un référentiel galiléen R considéré comme au repos. Il s’agit donc d’une force inertielle. Elle s’exerce perpendiculairement au mouvement d’un corps matériel dans ce référentiel en rotation et est proportionnelle à la vitesse de ce corps dans R’ ainsi qu’à la vitesse angulaire de rotation du référentiel R’ dans R. Ce n’est pas bien compliqué concernant le résultat empirique. Au-niveau mathématiques….
Quand un objet bouge dans un système de référence en rotation, il expérimente une force fictice appelée force de Coriolis, qui agit perpendiculairement à sa vitesse. Cette force fait que la trajectoire de l’objet se dévie, ce qui donne l’impression qu’il suit une courbe.
Ce phénomène trouve son origine dans la rotation de la Terre et sur son influence sur les objets en mouvement. Imagine que tu te trouves sur la Terre et que tu observes le mouvement d’un objet en ligne droite. De ton point de vue, l’objet semble se déplacer en ligne droite sans aucune déviation. Cependant, du point de vue d’un observateur situé dans l’espace, il verra que cet objet suit une courbe. Cette déviation est due à la rotation de la Terre. Et oui !
La force de Coriolis se manifeste par une force fictive agissant perpendiculairement à la vitesse d’un objet en mouvement dans un référentiel en rotation, comme la Terre. Dans l’hémisphère nord, cette force dévie le mouvement vers la droite, tandis que dans l’hémisphère sud, elle le dévie vers la gauche.
Il est important de noter que la force de Coriolis ne se manifeste que pour des objets se déplaçant sur de grandes distances ou à des vitesses importantes. Dans notre vie quotidienne, nous ne le remarquons pas dans les objets courants car son effet est très faible.
Allez, on anime tout ça.
La force de Coriolis a des effets sur plusieurs phénomènes naturels différents. Pour exemple, sur Terre, la force de Coriolis influe sur la direction des vents et des courants océaniques.
L’effet Coriolis peut se résumer simplement. Tout corps subira une déviation vers la droite de son mouvement dans l’hémisphère nord, vers la gauche dans l’hémisphère sud. Celle-ci est essentiellement visible à grande échelle et est d’autant plus marquée que l’objet circule vite et loin de l’équateur.
L’effet de Coriolis intervient à chaque fois que l’on considère un mouvement par rapport à un référentiel en rotation.
C’est donc quelque chose qui arrive :
- quand on marche sur un manège qui tourne
- quand on considère une fusée vis-à-vis d’un astre en rotation
- quand on regarde le déplacement des masses atmosphériques par rapport à la rotation de la Terre.
Les déviations de Coriolis des masses d’air finissent par mettre les dépressions en rotation et à former un cyclone rotatif.
Plus de détails sur ce que sont les tempêtes appelées ouragans, typhons, cyclone, en fonction de la région géographique d’où elles proviennent et de l’effet de Coriolis sur eux par ce petit film de 4’06 » très bien réalisé.
Et comme je t’en vends 2 pour le prix d’1, voici un autre petit film de 3’59 » pour voir la force de Coriolis autrement et son influence sur les cyclones, ouragans, etc… très intéressant !
Bon, on pourrait encore beaucoup en dire. Par exemple, on pourrait se demander par rapport à quoi le pendule de Foucault est fixe ? Et oui, à l’époque de Foucault, il existait un espace absolu par rapport auquel tous les mouvements sont définis. Cet espace immuable était donc un référentiel naturel pour l’oscillation du pendule.
Mais aujourd’hui, ma cousine préférée, l’espace ou plutôt l’espace-temps d’Einstein est une entité dynamique et la théorie de la relativité postule qu’il n’existe aucun référentiel privilégié. Dans l’univers le mouvement absolu n’existe pas, il est toujours relatif à un autre repère qui lui aussi est en mouvement. Pourtant on constate que le pendule de Foucault privilégie un référentiel précis puisque son plan indique une direction. Mais alors, par rapport à quoi le plan du pendule est fixe ? Et bien, tu vois, cette énigme n’est toujours pas résolue, et est toujours sujette à controverse.
Mais il faut savoir s’arrêter, ami passionné. Trois parties pour l’article sur le pendule de Foucault, c’est déjà bien…
A la prochaine !
Bye bye
Professeur Têtenlair
1,055 total views, 8 views today
La fonction « Répondre » étant épuisée, je réponds ici à mon ami passionné « tintin » de son post du 11 janvier 2025 à 6h58.
Salut tintin,
Comme tu le sais je ne réponds plus aux platistes qui me les gonflent au maximum avec leurs affirmations stupides, et en absence totale du moindre début de preuves. Le déni, rien que le déni, et pas l’ombre de la moindre preuve de leur pensée délirante.
Si la Terre était plate, je pense que oui (je n’ai aucune preuve à te fournir), le pendule aurait toujours son mouvement.
Par contre, ce qui est sûr, c’est que son aspect « déviant », « pivotant » n’existerait plus. Celui-ci étant lié à la force de Coriolis, inexistante sur une Terre plate sans rotation > plus d’effets « déviant » ni « pivotant ».
Ces idiots de platistes ont fait une vidéo pour « démontrer » l’imposture du pendule de Foucault. Je n’ai rien compris. Si tu comprends quelque chose, merci de me l’expliquer !
https://www.youtube.com/watch?v=ZHmpfzUVORk
Est-ce que le Pendule de Foucault et la Force de Coriolis auraient un rapport avec le Principe de Mach qui, si ma mémoire est bonne, expliquerait les phénomènes liés à la force centrifuge et à l’inertie?!…
RÉPONSE À MON AMI BERNARD 1/2
Pour une bonne compréhension de nos lecteurs, précisons ceci :
– Qu’est-ce qu’un corps inertiel ?
C’est un corps qui ne subit aucune force extérieure et qui ne présente ainsi aucun changement dans son état (au repos ou en mouvement de ligne droite). C’est le principe d’inertie de Newton.
– Le principe de Mach établi le contraire de ce qui précède : tous les objets de l’Univers sont en interaction, et donc un objet présente une inertie en fonction de toutes les autres masses dans l’univers.
Pour MACH Ernst (1838-1916), l’univers est un tout dans lequel tout est interconnecté quel que soit la distance entre les objets.
Albert Einstein a été très intéressé par ce principe pour sa Relativité Générale.
Pour Mach, « l’Univers est un tout dans lequel tout est interconnecté, quel que soit la distance entre les objets »… C’est étonnant pour l’époque, car c’est exactement ce qu’affirme la Mécanique Quantique! Et qui semble bel et bien avoir été confirmé, depuis la légendaire expérience d’Alain Aspect sur l' »Intrication Quantique »…et qui lui a valu le Prix Nobel de Physique en 2022.
Absolument ami.
Pour compléter ton information, si besoin était (!), je t’invite à lire mon très modeste article sur « La physique – mécanique et l’intrication quantique » en trois partie :
Partie 1 :
https://resistancerepublicaine.com/2022/10/26/la-physique-mecanique-et-lintrication-quantique-simplement-expliquees-1-sur-3/
Cette partie commence par le prix Nobel de physique 2022 qui a été accordé aux trois chercheurs pour leurs travaux en mécanique quantique, le Français Alain Aspect (que tu cites), l’Américain John Clauser et l’Autrichien Anton Zeilinger.
Partie 2 :
https://resistancerepublicaine.com/2022/11/09/la-physique-mecanique-et-lintrication-quantique-simplement-expliquees-2-sur-3/
Partie 3 :
https://resistancerepublicaine.com/2022/11/22/la-physique-mecanique-et-lintrication-quantique-simplement-expliquees-3-sur-3/
« Théorie des Supercordes », « Theorie M », « Théorie de la Gravité à Boucles »…nos Physiciens Théoriciens ne semblent guère à court d’idées pour tenter d’expliquer l’Univers et ses Lois!… Dernièrement, les super-puces Quantiques de Google, telles que « Sycamore » et « Willow », auraient exhibé des comportements autonomes…dignes d’un être vivant et conscient, et liés peut-être à l’existence d’un « Multivers »! Un tas de vidéos très récentes à ce sujet… A tel point que Google a choisi de mettre brutalement fin à l’expérience! Un Super-ordinateur Quantique pourrait-il avoir une Conscience…et même une Âme??! Il appartiendra à nos générations futures de répondre à cette question…qui pose d’énormes problèmes métaphysiques, et même moraux et éthiques! En tous cas, Arthur C. Clarke avait bien prédit tout çà, avec le Super-ordinateur « HAL-9000 », dans « 2001: L’Odyssée de l’Espace »…
RÉPONSE À MON AMI BERNARD 2/2
« Est-ce que le Pendule de Foucault et la Force de Coriolis auraient un rapport avec le Principe de Mach ? »
Je ne peux pas répondre à ta question, car je n’ai pas la réponse et, à ma connaissance, il n’y en a pas encore. La force de Coriolis est bien établie et démontrée.
Le principe de Mach n’est pas, à ma humble connaissance, scientifiquement démontré. Mach disait lui-même des théories et principes : « Il n’existe aucun principe intangible, les conceptions qui paraissent les plus fondées et les plus sûres ne sont que provisoires et peuvent être modifiées si l’expérience l’exige ». Ou encore : « L’objet de la science est la connexion des phénomènes ; mais les théories sont comme des feuilles mortes qui tombent quand elles ont cessé depuis longtemps d’être les poumons de l’arbre de la science ».
Mach rejetait toute hypothèse et ne se fiait qu’à l’observation. C’est pourquoi il a toujours refusé la notion d’atomes démontrés mais jamais observés.
Il aurait changé d’avis à notre époque, puisqu’on peut voir directement les atomes avec un Microscope Electronique puissant!… Quand à moi, la Physique m’intéresse depuis des décennies, surtout la « Physique de l’Extrême »…et j’aurai rêvé de travailler dans de beaux Centre de Recherches avancées, tels que ceux de Los Alamos, Lawrence Livermore ou Sandia, aux Etats-Unis! Avec Donald TRUMP désormais au pouvoir, j’y songe même très sérieusement!…
« Our Mission »:https://www.youtube.com/watch?v=fmP-ymRhI9U
« Stockpile Stewardship »:https://www.youtube.com/watch?v=8MmujbPYT80&t=76s
J’espère que tes voeux pourront se réaliser. C’est ce que je te souhaite pour 2025 !
Merci de ta participation à ce forum.
Merci à toi, Cachou! Pour moi ce sera les Etats-Unis…ou pourquoi pas, la Russie, et peut-être y travailler dans les Centres de Recherches d’Arzamas-16 ou de Chelyabinsk-70(VNIIEF ou VNIITF)!… Cà pourrait être formidable aussi!
http://www.vniief.ru, https://vniitf.ru/en
Ton « peuchère » provençal ajoute une touche locale
À ce fait universel que Foucault a prouvé,
Ta prose légère rend la physique joviale
Et même les plus sceptiques se trouvent captivés.
Merci professeur !
Je ne sais pas pourquoi, mais à chacun de tes poèmes j’éclate de rire. Non pas qu’ils soient risibles, car ils sont intéressants et bien construits. C’est, probablement, le contraste avec d’autres posts plus sérieux ??
Merci de tes encouragements,……….. peuchère !!
Allons allons, le livre est pourtant clair : la terre est plate, le soleil s’éclaire chaque matin et tombe le soir dans un lac de boue. Et en outre il faut égorger les infidèles ! C’est ça que nos collabos laissent professer chez nous ! Ensuite vous vous étonnez des conséquences… Que voulez vous les émirs sont si généreux avec nos zélites…
👍👏
Bravo pour ces trois cours ! Bravo sur le fond (c’est très clair) et aussi sur la forme (c’est très plaisant à lire). Quant à ta « cousine préférée, l’espace ou plutôt l’espace-temps d’Einstein », j’attends avec impatience un cours dessus, …mais en te recommandant de ne pas exagérer sur les tenseurs métriques et les dérivées covariantes… Ce sujet est chaud, pas évident à comprendre, et j’attends avec intérêt de voir comment tu vas t’en sortir (mais je te fais déjà confiance !)
Merci de ton post, ami Henri, qui m’a bien fait rire.
Cela dit, la théorie de la Relativité Générale a été modestement expliquée par ton serviteur sur RR en 6 parties.
Partie 1 : https://resistancerepublicaine.com/2021/11/24/la-relativite-generale-dalbert-einstein-et-oui-partie-1/
Partie 2 : https://resistancerepublicaine.com/2021/12/01/la-relativite-generale-dalbert-einstein-et-oui-partie-2/
Partie 3 : https://resistancerepublicaine.com/2021/12/08/la-relativite-generale-dalbert-einstein-et-oui-partie-3/
Partie 4 : https://resistancerepublicaine.com/2021/12/22/la-relativite-generale-dalbert-einstein-et-oui-partie-4/
Partie 5 : https://resistancerepublicaine.com/2022/01/05/la-relativite-generale-dalbert-einstein-et-oui-partie-5/
Partie 6 : https://resistancerepublicaine.com/2022/01/19/la-relativite-generale-dalbert-einstein-et-oui-partie-6-et-derniere/
Effectivement : six articles que tu avais écrits entre fin 2021 et début 2022, et que je n’avais pas encore lus : le temps s’est donc écoulé plus lentement dans ton référentiel que dans le mien, ce qui prouve une fois de plus que Einstein avait raison ! Merci, cher professeur !
😂
Bonjour, cher professeur, j’ai le cou raide ce matin. La force de Torticoriolis sûrement. Merci pour ce cours brillant.
😂 Merci de tes encouragements.
Heureusement que l’on ne ressent pas la rotation de la terre, on aurait le tourni. Par contre, si la rotation était verticale, aurions-nous conscience d’avoir la tête en bas par certains moments de la révolution.
Je me demande si à l’Equateur, la gravité terrestre pourrait être légèrement plus faible qu’aux latitudes moyennes et polaires, en raison de la force centrifuge due à la rotation de la Terre?! Un tel effet serait-il mesurable?…
Merci, ami Bernard de l’intérêt que tu portes à mon modeste article. Tu poses également des questions fort intéressantes comme celle de savoir si la gravité terrestre était légèrement inférieure à l’équateur par rapport au pôle ou aux latitudes intermédiaires ?
La réponse est oui. La Terre n’est pas une sphère parfaitement ronde elle est légèrement ellipsoïde car légèrement aplatie au pôle. Ainsi la distance entre le centre de la Terre (responsable de la gravité) et l’équateur est un peu plus grande que celle du centre de la Terre et des pôles.
De même, comme tu le signales très justement, la terre tourne à 1 600 km/h à l’équateur (à Paris un peu plus de 1 000 km/h) et donc la force centrifuge on est évidemment plus forte, ce qui diminue la gravité à l’équateur également.
Bien entendu que la différence de gravité entre l’équateur et les pôles est mesurable. A l’équateur elle est d’environ 9,78 m/s2 et au pôle d’environ 9,83 m/s2. Concrètement, que cela veut dire ?
Si tu lâches un objet lequel, dans son nouvel état, sera en chute libre, sa vitesse d’accélération (due à la pesanteur) sera une de celles ci-dessus citées où intermédiaires selon la latitude où tu te trouveras.
Tous ceux qui habitent dans l’hémisphère sud ont la tête vers le bas et de plus en plus quand il se rapproche du pôle sud. Mais ils n’ont ni plus ni moins de sensations que nous-mêmes, habitant dans l’hémisphère Nord.
Par contre il existe un grand nombre d’individus habitant dans l’hémisphère nord et qui ont la tête en bas et les pieds en l’air. On les appelle gauchistes, wokistes, LFI, macroniens, flanbysiens, et bien d’autres encore.
Merci cachou ! La boucle est bouclée encore un super article magistral et passionnant! On savait déjà que la terre tourne, maintenant on sait pourquoi. Je te souhaite une bonne année et surtout une bonne santé.
Je suis très honoré, Le chti français, que tu ais apprécié ces 3 volets du pendule de Foucault. Venant de ta part, ce n’est pas un mince compliment….
Bonjour Monsieur, vous serait-il possible d’effectuer le même type de raisonnement avec une terre plane s’il vous plaît 🙏 merci d’avance
Bon, les platistes, vous commencez à me fatiguer. Par respect pour vous, je vous ai répondu à plusieurs reprises. À chacun de mes articles parlant de la rotondité de la Terre, paf, le platiste de service me sort toujours sa petite rengaine.
Je vous ai répondu 1 000 fois que la démonstration de la rotondité de la Terre a été faite 1 000 fois.
J’attends toujours la démonstration des platistes de service de me faire les mêmes démonstrations pour démontrer que la terre est plate. J’attends toujours.
Je crois qu’à l’avenir, ce sont eux qui pourront désormais attendre mes réponses car il n’y en aura plus sur ce sujet.
Avec une terre plate nous aurions un sérieux problème de gravité .La gravité partant du centre de la terre et s’exerçant de manière identique sur chaque millimètre carré de notre chère planète. Avec une terre plate la gravité s’exercerait sur les cotes attirant tout vers le centre nous marcherions en biais , nos constructions seraient bancales tout comme l’ esprit des platistes . Question bête au prof tetenlair mais sérieuse, si cela était vrai le pendule de foucault pourrait-il même seulement amorcer son mouvement de balancier .