Pour relire (ou lire) la première partie, c’est ici.
La deuxième loi de Kepler
Elle est appelée « Loi des aires ».
Cette loi démontre que le rayon vecteur qui relie le centre de la planète au foyer décrit des aires égales en des temps égaux. T’inquiète paupiette, tu vas comprendre. Regarde le schéma ci-dessous.
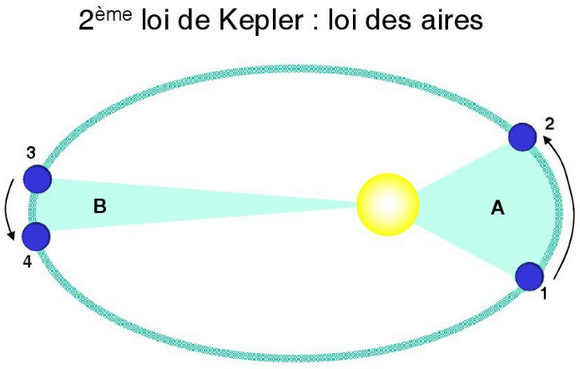
Tu reconnais l’ellipse. En jaune le soleil qui occupe un des foyers. Une planète suit donc son trajet elliptique. Elle passe obligatoirement lors d’une révolution (parcours complet de l’ellipse) par quatre points, 2 qui sont les plus proches du soleil (périhélie) et 2 qui sont le plus éloigné du soleil (aphélie).
Les 2 points les plus proches du soleil sont notées sur notre schéma 1 et 2, et les plus éloignées sont notées 3 et 4. Lors de sa révolution, la planète va mettre un certain temps pour franchir la distance de 1 à 2, et un autre temps pour franchir la distance de 3 à 4.
Kepler a observé, calculs mathématiques à l’appui évidemment, que le temps mis par la planète pour aller de 1 à 2 est le même que celui mis pour aller de 3 à 4. Pourtant la distance de 1 à 2 est bien plus importante que 3 à 4.
Également, les aires (surfaces) de la planète au Soleil sont de surfaces égales (même si leurs formes sont différentes), représentées sur le schéma par l’air A et l’aire B.
Quel est donc l’intérêt de cette deuxième loi dite Loi des aires ? Et bien il est extrêmement important, car il démontre de façon évidente que la vitesse d’une planète devient plus grande lorsque la planète se rapproche du Soleil. Cette vitesse est maximale au voisinage du rayon le plus court, le périhélie. Cette vitesse devient au contraire minimale au voisinage du rayon le plus grand, c’est-à-dire l’aphélie.
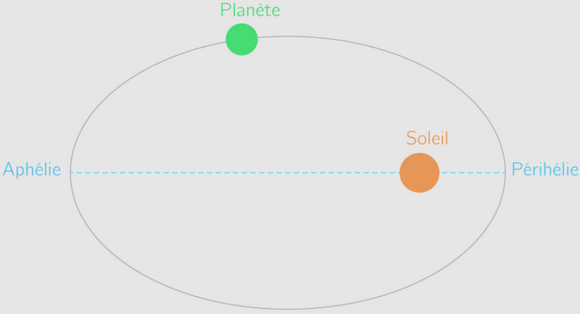
Les planètes en s’approchant du soleil accélère leur vitesse et en s’en éloignant ralentissent leur vitesse. La vitesse d’une planète sur son ellipse n’est donc pas constante.
Ainsi, le Soleil exerce une force puissante attractive des planètes vers lui. Nous savons que plus un objet tournant autour d’un point fixe est proche de ce point fixe, plus il tournera vite. A contrario, plus un objet est éloigné d’un point fixe en lui tournant autour, moins il ira vite. Le soleil a donc à une force d’attraction, de gravité, qui fait que la planète se rapprochant de lui accélère sa vitesse.
La troisième loi de Kepler
Elle est appelée « loi des périodes » ou « loi harmonique »
En 1619, Johannes Kepler publie le Harmonices Mundi (« L’Harmonie du monde » en cinq livres) dans lequel il fait un lien entre l’astronomie et la musique (ton serviteur est aux anges, puisque l’astronomie et la musique sont ses deux grandes passions !).
Dans cet ouvrage, il attribue aux planètes un thème musical. Les variations des vitesses de ces planètes sont représentées par les différentes notes composant la musique. Ainsi, il était facile de distinguer les orbites les plus excentriques. Ce qui est dit ici est exact, mais revenons à l’essentiel de cette troisième loi.
C’est dans cet ouvrage que Kepler énonce sa troisième loi fondamentale. Cette loi est une démonstration mathématique.
Le carré de la période de révolution est proportionnel au cube du demi-grand axe [de l’ellipse]. Celle-ci découle de ses recherches sur un modèle d’Univers harmonique. Cette loi permet de connaître la distance d’un corps au Soleil si on connaît sa période de révolution (=temps qu’il faut à la planète pour boucler son orbite). Celle-ci est relativement facile à mesurer alors que la distance l’est moins. Il y a donc un rapport constant entre la période de révolution et le rayon de l’orbite de la planète, donc sa distance par rapport au Soleil. On va essayer de la faire au plus simple.
Appelons le temps que met une planète pour faire sa révolution (le trajet complet de l’ellipse) T. Nous avons vu, dans la première partie, ce qui était le grand axe d’une ellipse. Pour rappel :
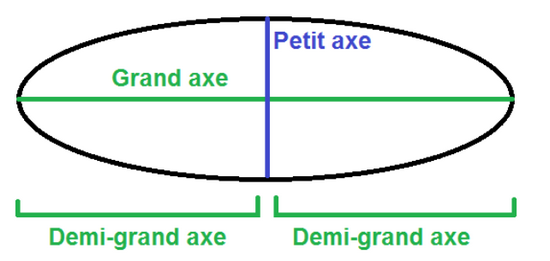
Le demi grand axe est représenté par le trait rouge de la figure ci-dessous :
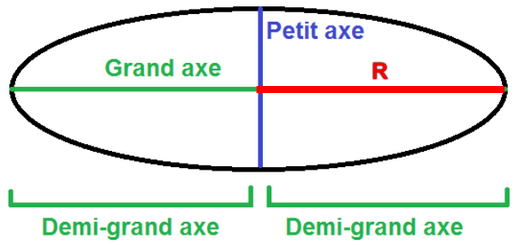
Nous nommerons ce demi grand axe R.
Le carré de la période de révolution est donc :
Le cube du demi-grand axe [de l’ellipse] est :
Et boum, on a la troisième loi de Kepler !
À partir du demi grand axe on peut déterminer la durée de révolution d’une planète, et réciproquement.
Oui, ami très curieux, tu vas me dire quelle est la constante ? Et bien pour cela il faut savoir que Newton a mis son grain de sel dans la formule de Kepler et l’a complétée. Cette constante souvent appelée K fait appel au carré du chiffre pi, à la constante de gravitation universelle G et enfin à la masse de l’astre central M autour duquel tourne les planètes ou satellites.
On a ainsi une constante comme suite :
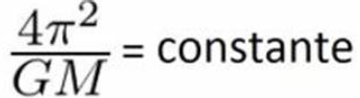
Ce qui nous donne la formule finale :
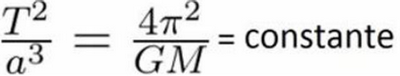
Dans cette formule le a = R du dessus
Et voilà, le tour est joué. À partir de là on peut connaître beaucoup de notions sur les planètes, dont la distance d’un corps au Soleil si on connaît sa période de révolution, et plein d’autres choses.
Voilà, ami désireux d’en savoir toujours plus, les trois lois de Kepler qui régissent le mouvement des planètes encore aujourd’hui.
Bye bye !
1,349 total views, 1 views today
Salut Cachou !
j’ai bien compris la première partie
C’est évident que la vitesse d’un corps s’accélère à l’approche du Soleil !
Pour la 2ème partie, là pour moi, c’est plus hardi !
Faut dire que je ne suis pas très fort – même très faible – en mathématique
Mais bon, des gars comme Kepler – et toi – sont là pour pallier à nos manque !!
Pour terminer ,une question : est que la terre en période d’été est au plus proche du soleil , ou est ce l’inverse ?
🙂
Cela fait un an que je me posais la question de savoir si j’écrirai un article ou non sur les trois lois de Kepler. Pour une seule raison : la troisième loi est uniquement mathématique. L’objectif de RR et le mien, et de faire des articles qui intéressent et simples à comprendre. D’où mes hésitations.
D’un autre côté, être responsable d’une rubrique sur l’astronomie et ne jamais parler des lois de Kepler, sur lesquelles repose encore les mouvements des planètes, paraît difficile.
Je l’ai donc fait, en simplifiant à l’ultra possibilité les formules mathématiques de la troisième loi.
Je réponds maintenant à ta question : «Est-ce que la Terre en période d’été est au plus proche du soleil , ou est-ce l’inverse ? ». Lire mon post suivant.
Pas de problème , c’est bon
Même si je suis un cancre en mathématique, j’admire cela ! ( les maths, hein, pas le cancre… :o)
Et je comprend quand même le sens général !
Et puis on ne peut pas faire l’impasse , comme tu le dit
C’est la science, notre bonne science !
Réponse à ta question du post précédent.
Ni l’un, ni l’autre. La distance de la Terre par rapport au Soleil n’a strictement aucune répercussion sur températures terrestres. C’est uniquement l’axe de rotation qui est oblique (23.4° par rapport à la verticale) qui influence la chaleur sur notre planète.
La chaleur est due uniquement au niveau d’inclinaison des rayons solaires par rapport à notre Terre qui tourne sur elle-même et dont son axe n’est pas vertical.
À telle enseigne que le 02/01/2021 la Terre s’est trouvée à son périhélie (distance la plus courte par rapport au Soleil) et nous étions en plein hiver !
Tu me donnes une idée d’article, et je vais traiter toutes ces questions assez détaillées, les saisons, les différences de température, la variation de la durée des jours, équinoxes, solstices.
Mon prochain article du 20/07/2022 porte sur le nano satellite appelé PicSat, la très jeune étoile appelée Bêta Pictoris et l’exoplanète (planète située hors du système Solaire) appelé Bêta Pictoris b.
Le 03/08/2022 je traiterai des questions dont nous avons parlé ci-dessus. Merci à toi ami.
Ok !
Donc pas d’influence – notoire du moins – de la distance pour les température
Remarque c’est valable pour la terre car je suppose que l’écart de distance n’est pas trop important entre la périhélie et l’aphélie..
Mais si nous étions dans l’orbite de Vénus ou pire Mercure… :o)
Bien entendu , c’est l’inclinaison de l’axe terrestre, la première cause..
Tes prochains sujets sont alléchants !
que de noms poétiques !!
Un nano satellite !? Qu’est donc que cette bestiole !?
les exo planètes, c’est super !
Alors oui, sus à Pictoris !
:o)
Il y a une petite influence de la révolution elliptique de la Terre sur les saisons mais elle est mineure. L’essentiel des saisons est l’axe oblique de la Terre de 23°.
D’ailleurs je me suis attelé à l’article dont tu m’as donné l’idée et il est déjà bien avancé. Comme déjà dit, il sera publié le 03/08/2022. Je vais bientôt le terminer, le peaufiner et le relire cinq à six fois comme toujours.
Lorsque la Terre et au périhélie (la plus proche du Soleil) elle est environ à 147 millions de kilomètres. Lorsqu’elle a fait un demi-tour de sa révolution et se trouve à l’opposé, donc la plus éloignée du Soleil (aphélie), elle est à environ 152 millions de kilomètres. Le delta est donc d’environ 5 à 6 millions de kilomètres, ce qui est extrêmement peu. Mais nous savons que l’ellipse de l’orbite de la Terre est presque circulaire, d’où cette très faible distance entre le périhélie et l’aphélie.
Merci à toi
Ok !
bien réçu
la suite au 3 aout…
J’aimerai bien savoir écrire comme toi !
Tu as songé à te lancer dans l’écriture de roman de science fiction, en partie bien réaliste, avec tes connaissance dans l’astronomie, astronautique , etc ? !
;o)
Merci de nous régaler !
Je pense aussi à un ouvrage passionnant : « Kepler, Le Visionnaire De Prague » de Henriette CHARDAK – Emission de 2004 à écouter dans les archives (Radio Ici et Maintenant) :
https://archive.org/details/JohannesKepler
Merci Jules. Je vais écouter ce postcast, comme on dit maintenant, avec beaucoup d’intérêt.
Question: Si le soleil attire les planètes qui gravitent autour de lui, pourquoi celles-ci parviennent encore à échapper à son attraction? Entre nous, cela m’arrange … Merci aussi de nous expliquer ces formidables mystères de l’Univers, très difficile exercice de vulgarisation.
Merci de ta question, ami gigobleu.
C’est la force d’inertie qui permet cela. Il s’agit de l’égalité entre l’effet centrifuge et l’effet centripète (gravitation du Soleil) lors d’une planète tournant autour du Soleil, tout simplement.
Pour que les planètes chutent vers le Soleil, il faudrait affaiblir leur énergie cinétique. Seul Dieu est en capacité de le faire actuellement. Macron, Véran, Ursula von der Leyen, Moussa Darmanin, et bien d’autres le feraient bien volontiers pour anéantir la planète comme ils le souhaitent. Mais ils n’y arrivent pas encore… Mais comme les français votent mondialistes depuis 50 ans, et qu’ils continueront de le faire jusqu’à la suppression totale des élections, peut-être que la chose se fera ???
Bonjour,
Merci pour cet article !
👍