
PARTIE 4
Pour relire (ou lire) la première partie de notre exposé, c’est ici.
Pour relire (ou lire) la deuxième partie de notre exposé, c’est ici.
Pour relire (ou lire) la troisième partie de notre exposé, c’est ici.
NOTION D’ESPACE-TEMPS
Au tout début du XXe siècle Albert Einstein bouleverse notre conception du temps et de l’espace. Il annonce que les masses – celle d’une planète, d’une étoile par exemple ou d’une galaxie– déforment l’espace. Et oui, ma cousine : déforme l’espace ! C’est pas rien ça ! Mais attends, ce n’est que le début ! De fait, pour le représenter il faut plutôt s’imaginer un trampoline dans lequel “s’enfoncent” les astres plus ou moins massifs qui le jalonnent.
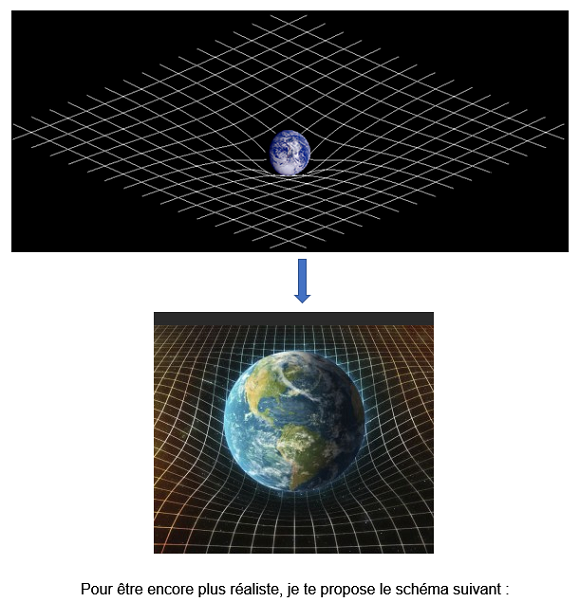

En fait, ce shéma est plus réaliste que le précédent, car ce dernier laisse croire que l’espace est plat et que la masse ne fait que tomber dans un creux en tirant la « grille » vers le bas. Ce n’est pas ce qui se passe : il n’y a pas de haut et de bas dans l’espace, et de plus, les déformations dans l’espace-temps ne se font pas sur un seul plan, mais dans tous les plans. C’est ce que l’on appelle les “ondes gravitationnelles”. Regarde cette petite animation ci-dessous qui explique bien aussi la chose :

POURQUOI LA TERRE TOURNE-T-ELLE AUTOUR DU SOLEIL ?
Par la déformation de l’espace-temps
Jusque-là, nul ne se posait la question de la forme de l’espace qui était considérée lisse comme une feuille de papier. Ainsi ce que Newton appelait la force gravitationnelle n’est rien d’autre que la déformation de l’espace. Par ailleurs, alors que Newton n’établissait aucun lien entre l’espace et le temps, Einstein émet l’idée de l’espace-temps.
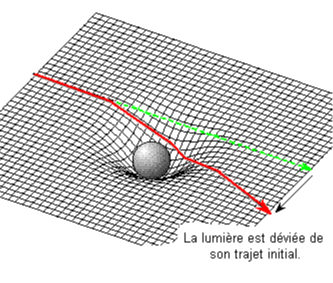
Einstein part du principe que la lumière est la vitesse maximum possible, 299 792 458 m/s environ 300 000 km/s, ce qui est évidemment vrai, est le principal messager des astres. On ne voit les étoiles, le Soleil, que par la lumière qu’ils nous envoient. Et bien Einstein a établi que la lumière, que l’on croit absolument rectiligne, se courbe au passage des corps céleste tout comme l’espace. Elle se déplace ainsi en suivant la courbure de l’espace à la vitesse finie de 300 000 Km/s. Or, la forme de l’espace est précisément ce qui détermine le temps de trajet de la lumière. Si l’espace n’est pas déformé, la lumière va en ligne droite. Si l’espace est déformé par des corps célestes, et bien la lumière qui se meut dans l’espace suivra la forme de ce dernier et se déformera aussi. C’est donc ainsi que depuis Einstein, l’espace se trouve à jamais être relié au temps, pour créer « l’espace-temps ». Alors, t’es pas ébahi, mon ami ?
 Devant un tel bouleversement, Einstein lui-même fournit quelques moyens de tester sa théorie qui suscitait tant d’incrédulité. L’un des tests proposés pouvait se dérouler… pendant une éclipse ! Un test facile à monter, et incroyablement bien imaginé car prenant le ciel entier comme un immense laboratoire. Il suffisait pour cela d’observer le Soleil et une poignée d’astres bien répertoriés ceux de l’amas des Hyades, par exemple. Or, au sein d’un amas, les étoiles présentent des distances angulaires fixes les unes par rapport aux autres. Mais, à un certain moment de l’année, en fonction de la position du Soleil dans le ciel, la lumière de quelques-unes de ces étoiles doit passer à proximité du Soleil avant de parvenir jusqu’à l’observateur terrestre.
Devant un tel bouleversement, Einstein lui-même fournit quelques moyens de tester sa théorie qui suscitait tant d’incrédulité. L’un des tests proposés pouvait se dérouler… pendant une éclipse ! Un test facile à monter, et incroyablement bien imaginé car prenant le ciel entier comme un immense laboratoire. Il suffisait pour cela d’observer le Soleil et une poignée d’astres bien répertoriés ceux de l’amas des Hyades, par exemple. Or, au sein d’un amas, les étoiles présentent des distances angulaires fixes les unes par rapport aux autres. Mais, à un certain moment de l’année, en fonction de la position du Soleil dans le ciel, la lumière de quelques-unes de ces étoiles doit passer à proximité du Soleil avant de parvenir jusqu’à l’observateur terrestre.
Or, si la relativité générale dit vrai, la masse du Soleil déforme l’espace et la lumière qui nous parvient de la part des étoiles de l’amas des Hyades, qui se trouvait à ce moment autour du soleil, prend un chemin différent. Conséquence : depuis la Terre, on devrait voir que l’amas des Hyades, cette grosse grappe de 400 étoiles située à quelques 150 années lumières, ne serait plus situé au même endroit que d’habitude. Et lors de l’éclipse du 29 mai 1919, ceci a été vérifié !
En effet, ces étoiles n’étaient pas à leur place habituelle. Leur lumière, qui a voyagé 150 ans pour nous arriver, a été détournée, pliée, juste avant d’arriver sur la Terre, par l’attraction du Soleil. De presque rien, 1,75 seconde d’arc, soit l’angle formée par un triangle rectangle de 2,5 cm de haut sur… 3 km de long. C’est exactement ce qu’avait prédit et calculé Albert Einstein.
Le lendemain, le savant était à la Une de la plupart des quotidiens, qui soulignaient à l’époque que personne n’avait encore réussi à expliquer clairement au grand public ce que signifiait cette théorie de la relativité.
Cette observation marque ainsi le triomphe de la relativité générale. Depuis, la théorie d’Einstein n’a jamais été prise en défaut.
Une autre façon de voir l’indissociabilité de l’espace et du temps
Cette notion est contre intuitive. Il faut s’y habituer. Et pourtant, on peut l’expliquer si simplement ! Quand tu te balades en forêt, tu te déplaces dans l’espace habituel et ses trois dimensions :
- hauteur : l’espace qui existe entre toi et le ciel
- largeur : l’espace qui existe entre toi et tous les arbres à ta droite et ta gauche
- profondeur : l’espace qui existe entre toi et tous les arbres devant et derrière toi
Bon, et le temps dans tout cela ? Et bien, quand tu avances, du temps s’écoule. Vicieuse comme tu es, tu vas me dire : “Et, ho, si j’avance pas, si je reste sur place, hein, gros malin ?”. Et bien, c’est pareil, la station immobile n’étant qu’un cas particulier de la vitesse où elle est à 0. Les trois dimensions continuent d’exister et le temps avec qui passe.
Tu fais marche arrière ? Pareil, les trois dimensions continuent d’exister et le temps continue d’avancer, même si tu marche en arrière. Les aiguilles de ta montre ne tourneront pas à l’envers !
Désormais, le temps est maintenant totalement indissociable de l’espace et ses 3 dimensions. On ne peut plus parler d’espace, mais systématiquement d’espace-temps dans 4 dimensions.
Une autre expérience-explication
Voici une autre explications au phénomène de déformation d’espace temps. Cette explication te montre que, en présence de gravité donc de masse, la ligne droite (appelée géodésique) n’existe pas. Faisons un graphique représentant l’altitude (sa position verticale dans l’espace) d’un objet en fonction du temps. Il représente donc une dimension de l’espace et le temps :
Imaginons que nous soyons dans une région de l’espace où il n’y a pas de gravité : l’espace-temps n’est pas déformé.
Si on pose un objet à une altitude donnée, cet objet restera à la même altitude au cours du temps. On peut représenter ça par une droite :
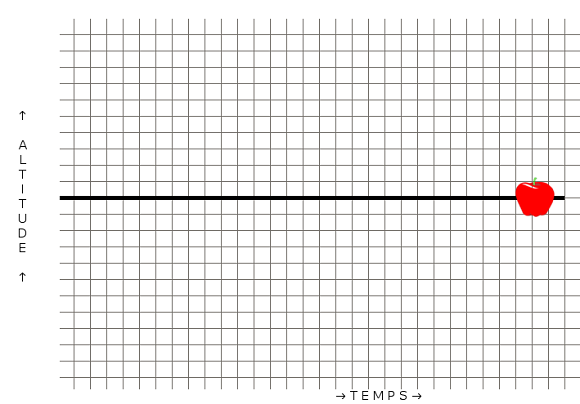
On voit que le temps qui passe n’a pas d’influence sur la position de l’objet dans l’espace.
Faisons intervenir la gravité. N’oublions pas que la gravité est maintenant une déformation de l’espace-temps. Déformons donc l’espace-temps :
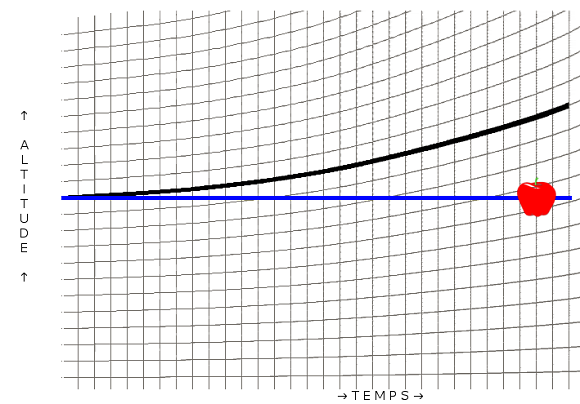
Note bien, mon cousin préféré, que ce ne sont pas les lignes du quadrillage qui sont déformées, mais l’espace-temps lui-même. Les lignes que tu voies courbées sont en réalité des lignes droites : c’est donc comme si la définition de la rectitude était elle-même déformée.
Regarde également que la pomme se déplace toujours en ligne droite sur le dessin, mais que dans la réalité, vu qu’elle ne suit pas les lignes droites (qui sont donc, en fait, non droites) de l’espace-temps, cette ligne bleue n’est plus droite.
Pour y voir plus clair, conservons la gravité mais redonnons un aspect artificiellement « droit » aux lignes droites de l’espace-temps et voyons ce qui se passe :
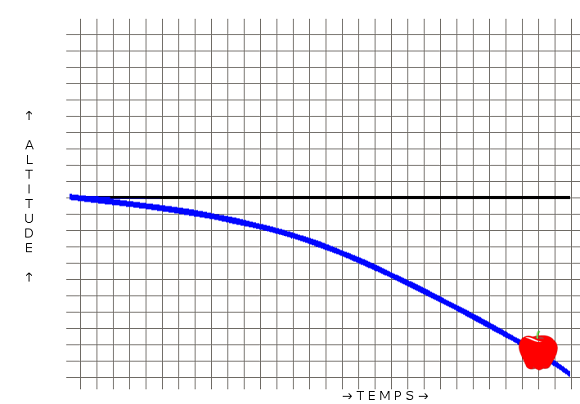
Et là, c’est très clair : les lignes droites de l’espace sont de nouveau droite, même avec la gravité, sauf que… la trajectoire de l’objet ne suit plus du tout les lignes de l’espace temps : elle descendent. La gravité a ainsi fait son effet : dans un champ gravitationnel (dirigé ici vers le bas), les objets voient leur positions également évoluer vers le bas, au fur et à mesure que le temps passe : l’objet tombe.
La déformation de l’espace temps est d’autant plus importante que le champ gravitationnel est intense, et donc que la masse qui produit cette déformation est importante.
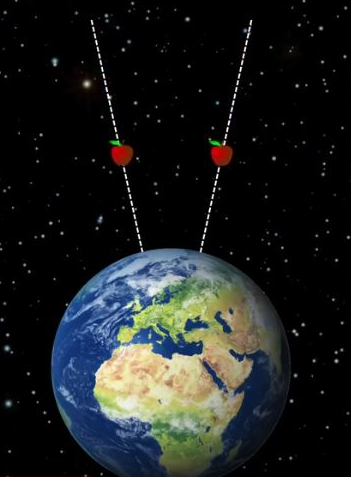 Allez, parce que c’est toi, encore une nouvelle (petite) explication que la ligne droite parfaite n’existe pas dans l’espace. Plus on voit la même chose sous différents aspects, mieux on la comprend. Si on lâche deux pommes séparées d’un mètre, elles vont tomber en apparence de manière rectiligne et parallèle. Mais si on les fait tomber de très loin au-dessus de la Terre, leur trajectoire va se courber vers le centre de la Terre (là où la masse gravitationnelle est la plus importante).
Allez, parce que c’est toi, encore une nouvelle (petite) explication que la ligne droite parfaite n’existe pas dans l’espace. Plus on voit la même chose sous différents aspects, mieux on la comprend. Si on lâche deux pommes séparées d’un mètre, elles vont tomber en apparence de manière rectiligne et parallèle. Mais si on les fait tomber de très loin au-dessus de la Terre, leur trajectoire va se courber vers le centre de la Terre (là où la masse gravitationnelle est la plus importante).
En clair : la masse courbe les trajectoires, les lignes droites parfaites n’existent pas, et des parallèles peuvent se rencontrer ou se rapprocher.
C’est ça qu’on appelle la courbure de l’espace, et qui est un des piliers de la relativité générale. Cette notion permet notamment de comprendre que le trajet le plus court d’un point à un autre n’est pas forcément la ligne droite apparente, selon la courbure de l’espace. Dans cette géométrie dite « non-euclidienne », où plus rien n’est plat, le théorème de Pythagore, par exemple, ne fonctionne plus du tout !
Bref, en découvrant et en utilisant la géométrie courbe pour expliquer la gravité, Einstein a fait un pas de géant dans la compréhension du monde qui nous entoure.
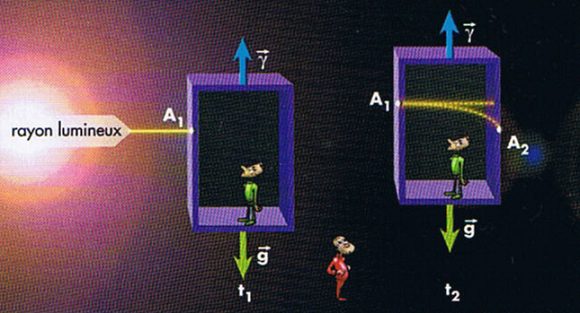
Enfin, dernière expérience, imaginée par Einstein lui-même : soit un ascenseur qui subit une accélération y dirigée vers le haut. Un observateur enfermé dans l’ascenseur croit être soumis à un champ de gravitation g dirigé vers le bas. A l‘instant t1, un rayon lumineux perpendiculaire pénètre dans l’ascenseur au point A1 et en ressort à l’instant t2. Pour l’observateur extérieur, le trajet est rectiligne. Pour l’observateur intérieur, le trajet du rayon est courbé.
Conclusion : la présence d’un champ gravitationnel courbe les rayons lumineux.
Finalement, ce que j’essai de t’expliquer, c’est qu’en fonction de la relativité générale, quand tu as la présence d’une masse, tu n’as pas ça :

Mais ça :

Bon, ben, ça fait déjà pas mal à digérer pour cette quatrième partie ! La prochaine fois, nous poursuivrons par « La dilatation du temps« . On s’en lèche déjà les babouines !!

ET

Professeur Têtenlair
2,426 total views, 1 views today


Excellente vulgarisation ! Ce qui est très difficile !
Bravo pour cet article !
Ooooh… j’apprends des choses concernant les étoiles : j’ignorais que les étoiles « changeaient de place ». (Ou plutôt, leur perception…!)
Pourtant, c’est logique au vu des explications fournies dans ces articles… mais je n’y avais jamais même pensé.
Il se dit que, si on arrivait à une vitesse supérieure à celle de la lumière, alors on voyagerait dans le temps.
Bon… techniquement, on « voyage » TOUS dans le temps… mais on se comprend!
J’aimerais bien comprendre ce que « voyager dans le temps » grâce à une vitesse supérieure à celle de la lumière impliquerait exactement : nous retrouverions-nous PHYSIQUEMENT dans le passé, ou bien dans une dimension parallèle qui nous permettrait d’être SEULEMENT témoin du passé – sans pouvoir y intervenir?
…Bon, je m’arrête là avant de partir dans des « délires »…
Merci pour cet article, et Joyeux Noël!!
Le seul avantage si on pouvait, comme tu le dis, nous retrouver « PHYSIQUEMENT dans le passé », c’est de retrouver notre beau pays et les belles mentalités de ses habitants d’antan.
Et surtout convaincre les gens de ne pas voter des imbécile-abruti-traitres successifs pendant 50 ans qui ne feront que détruire notre pays et mettrons en place le Grand Remplacement.
En un mot, convaincre les français de ne pas se suicider. Mais ça…c’est une autre histoire !
Il est à noter que c’est Paul Langevin qui a jeté les bases de la relativité. Einstein en s’inspirant de ces travaux a réussi à en faire une formulation mathématique.
Depuis, la théorie des cordes met quelque peu à mal la formulation d’Einstein.
De plus, dans la physique de l’infiniment petit et la découverte des plasmas, entre autres, la théorie de la relativité ne tient pas.
En fonction des échelles, il existe donc des modèles physiques et mathématiques différents.
Il aura fallu l’avènement de la physique quantique pour arriver à modéliser, de façon acceptable, tout ce qui rapport à l’atome.
Je pense que la théorie de la relativité, ainsi que la physique quantique sont a mettre au même niveau, quant à l’importance de ces découvertes.
Et merci pour ces articles, vous arrivez à expliquer de façon compréhensible, pour tout un chacun, des notions scientifiques extrêmement ardues.
En effet, depuis la théorie de la Relativité Générale, d’autres approfondissements sont apparus.
Je ne pense pas que cela la remette en cause, mais « l’encadre » peut-être, la rendant un peu moins « générale ».
Je pense que ce que tu dis est réaliste : « En fonction des échelles, il existe donc des modèles physiques et mathématiques différents. »
Il faut être un très grand spécialiste qui domine globalement toutes ces théorie-découvertes afin de les mettre en rapport les unes aux autres et les « replacer » dans l’espace-temps.
Ce que je ne suis évidemment pas !
Excellent cours. Ça donne le vertige. Pour moi le plus vertigineux c’est de penser que l’espace n’a pas de commencement dans le temps ni de fin, ni de limitation. Concevoir l’éternité de l’espace alors que je ne suis qu’ un être mortel me perturbe.Difficile à appréhender. Il n’y a pas de début du temps, ni de fin. Spinoza assimilait Dieu à l’étendue. Peut-être parce que l’étendue était infinie, comme les attributs de Dieu.Cela lui a valu bien des déboires.Bon j’arrête de philosopher et je te souhaite un joyeux Noël et une excellente années 2022.
« …que l’espace n’a pas de commencement dans le temps ni de fin… ».
Comme quoi, la maxime, « Tout a un début et une fin » n’est pas universelle.
Il y a une exception cependant : « Tout a une fin, sauf la banane qui en a deux. » 😉 (Proverbe Bambara).
Amitié, ami Argo et bon réveillon !